What is Simple Harmonic Motion (SHM)?

If an object is displaced from its stable/ equilibrium mean position, and a force starts acting on it such that:

• It tries to bring the object back to its mean position, i.e. the force is directed towards the mean position, and
• The magnitude of the force acting on the oscillating body is directly proportional to its displacement from the mean position.

Then such a motion is called Simple Harmonic Motion (SHM). It is the simplest kind of oscillatory motion.

In absence of a continuous external force working on an oscillating body, it will automatically come to rest at its equilibrium position in some time due to friction, air drag, and other dissipative forces.

Table of Contents

• Real-life examples of SHM
• Some Terminologies related to Simple Harmonic Motion

Any oscillating body has one equilibrium mean position, and two extreme ends. Let’s understand the parameters of the system at these two types of positions.

System parameters at mean position

When a point-size object executing Simple Harmonic Motion passes through the mean position:

• No force acts on the object. Obviously, it means that its acceleration would be zero.
• Its Velocity is maximum. So, obviously its Kinetic energy would be maximum, and its Potential energy would be minimum.

System parameters at extreme ends

When a point-size object executing Simple Harmonic Motion is at one of the extreme ends, then:

• Restoring force acting on the object is maximum. Obviously, it means that its acceleration would be the maximum.
• Its Velocity is zero. So, obviously its Kinetic energy would be zero, and its Potential energy would be maximum.

Real-life examples of SHM

Now, let’s have a look at some of the real-life systems that showcase Simple Harmonic Motion.

Note

In real-life no system executes absolutely pure simple harmonic motion. All these examples are as close to SHM as we can get.

Oscillations due to a Spring

Let us have a block of mass m fixed to a horizontal spring (or vertical spring), which in turn is fixed to a rigid wall. Also, let’s consider the surface on which the block has been placed as frictionless.

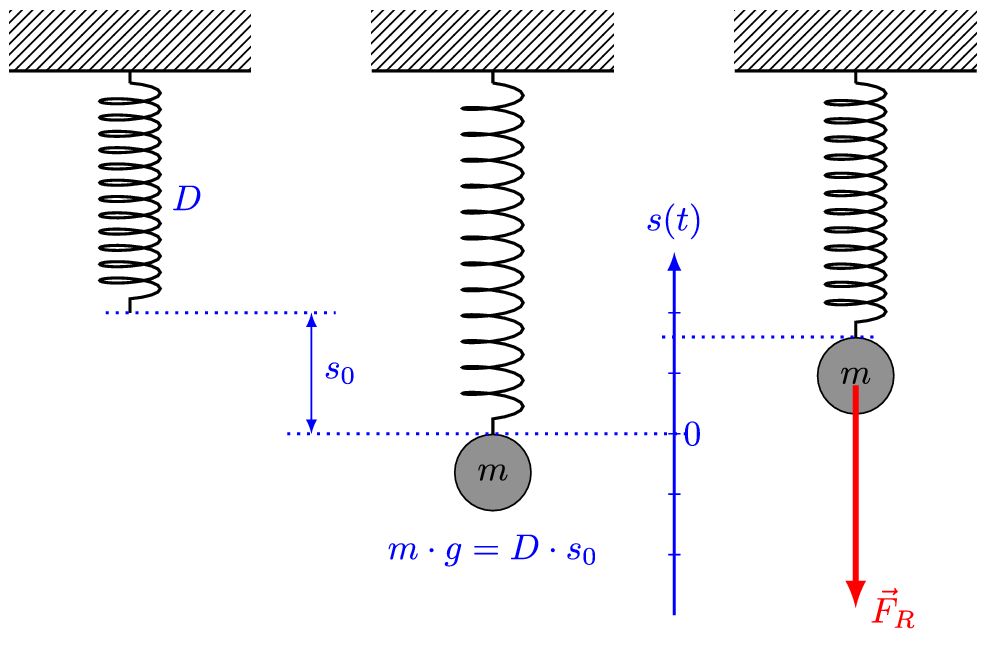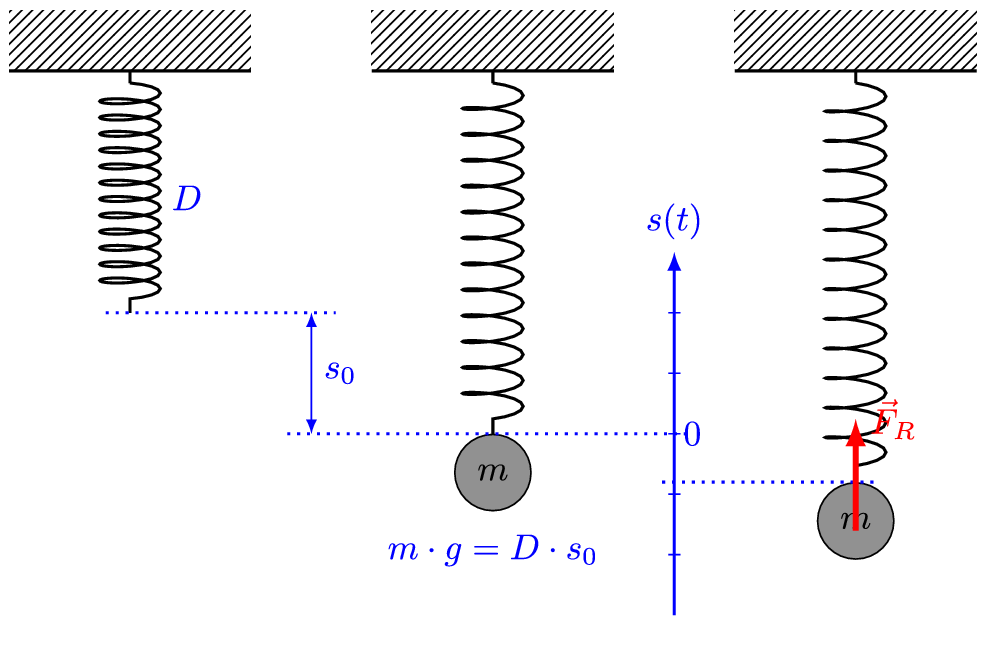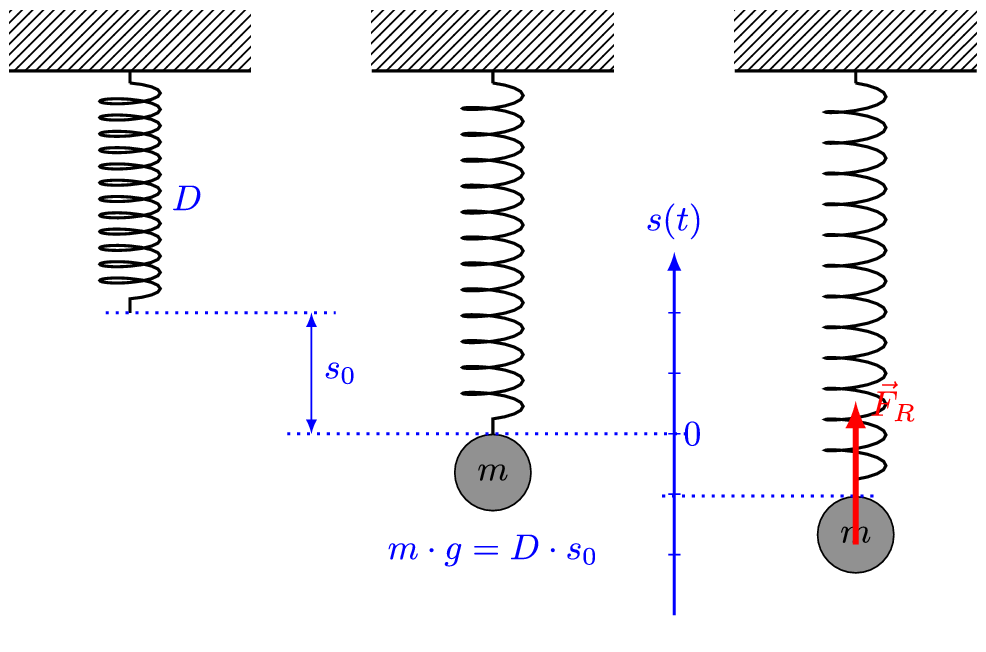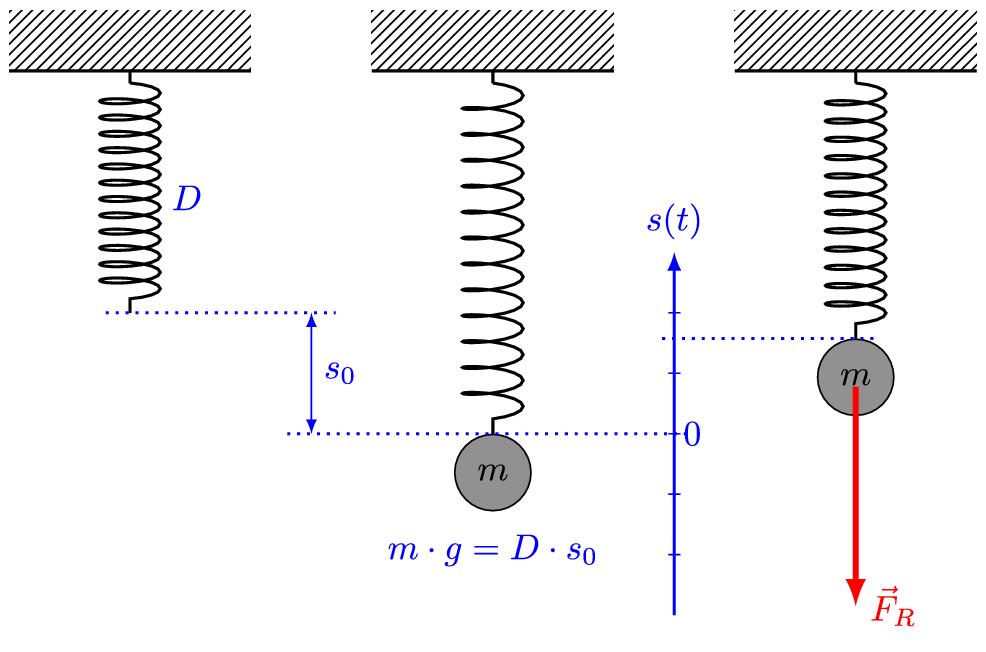
If we push or pull the block and then release it, it will execute a to and fro motion about a mean position, which is nothing but a simple harmonic motion. That is, it will act as a linear simple harmonic oscillator.

The reason behind it is simple. As discovered by English physicist Robert Hooke (and proposed as Hooke’s law), a spring when deformed, applies a restoring force. The magnitude of the restoring force is proportional to the deformation (i.e. the displacement of the block). The direction of this restoring force is always in the direction opposite to the displacement.

Simple Pendulum

Let us have a block of mass m suspended by a vertical thread, which in turn is fixed to a rigid ceiling. Also, let’s consider the space to be a vacuum, i.e. there is no air drag.

If we push or pull the block and then release it, it will execute a swinging motion about a mean position, which is nothing but a simple harmonic motion. This is nothing but a Simple Pendulum.

Some Terminologies related to Simple Harmonic Motion

Time Period

It is the time that a particular pendulum takes to complete one full oscillation. We use the symbol T to denote it. And as it measures time, its SI unit is obviously second.

Time period of any given simple pendulum, T = 2π√(L/g)

Where, L is the length of the thread and g is the acceleration due to the gravity.

Note

Keep in mind that the time period of a simple pendulum doesn’t depend upon the mass of the pendulum.

Special cases of Simple Pendulums

There are two special cases of Simple Pendulums worth noting.

• Simple pendulum of infinite length: If the length of the thread of a simple pendulum is made infinite, then its time period would be 84.6 min.

• Second pendulum: It is a Simple Pendulum whose time period is exactly 2 seconds.

Effect of L on Time Period

As g at any given place is almost constant, the time period of a given simple pendulum is only dependent on the effective length of the thread. Let’s see a few examples showcasing this fact.

• A pendulum clock gets slow in summer and fast in winter. That’s because in summer time the length of the thread (L) increases, which in turn increases the Time Period (T).
• If a child swinging on a swing stands up, then it would lead to the center of gravity (C.G.) of the body coming upward. This essentially means that the effective length of the swing (L) decreases. So, Time Period (T) of the swing will decrease too.

Effect of g on Time Period

Though g is almost constant at any given place, it may vary from one place to another. Can you guess the impact it would have on the time period of the simple pendulum?

Let’s see.

• If g is increased somehow (e.g. at earth’s poles, or when a lift is going up with accelerated motion), the time period of the simple pendulum will decrease, i.e. it will run faster.
• If g is decreased somehow (e.g. at earth’s equator, or when a lift is coming down with accelerated motion), the time period of the simple pendulum will increase, i.e. it will run slower.
• If g is made zero somehow (e.g. on an artificial satellite in space), the time period of the simple pendulum will become infinite (∞), i.e. it will stop working.

Frequency

Frequency of a simple pendulum is the number of oscillations completed by it in one second.

We use the symbol v to denote it. Its SI unit is hertz or \((second)^{–1}\).

Amplitude

We know that a pendulum swings about a mean position. The distance of a pendulum from this mean position (at any given time) is called its displacement.

Amplitude of a swinging pendulum is the maximum displacement from the mean position. Obviously, it would be equal on either side of the mean position.

We use the symbol a to denote it. Its SI unit is metre.

Phase

Phase of an oscillating particle is a physical quantity that expresses:

• its position, and
• its direction of motion.

We use the symbol Φ to denote it.

So, two oscillating particles may be at the same position, and yet in different phases if their direction of motion is different.

For example, consider two oscillating particles executing SHM that are at present at their mean position (so their position is same).

• If both of them are moving in the same direction too, then they will be considered to be in same phase (i.e., Φ = 0°).
• However, if they are moving in opposite directions, then they will be considered to be out of phase (i.e., Φ = 180°).