Spherical Mirrors

In this article, we are going to study about the concepts related to spherical mirrors, such as the kinds of images formed by them, their focal points, their uses, etc.

Table of Contents

• What are Spherical Mirrors?
• Real and Virtual Images
• Position and Nature of images formed by a Concave Mirror
• Position and Nature of images formed by a Convex Mirror
• Use of Spherical Mirrors

What are Spherical Mirrors?

Spherical Mirror is a cut part of a hollow glass sphere, such that one of its sides has been polished, and so the other side reflects the light falling on its surface.

Just imagine a standard plane mirror that has been curved.

There are two types of spherical mirrors:

• Concave mirror
  

• Convex mirror
  

Terms and Definitions related to Spherical Mirrors

Now, let’s have a look at some of the terms and definitions related to spherical mirrors.

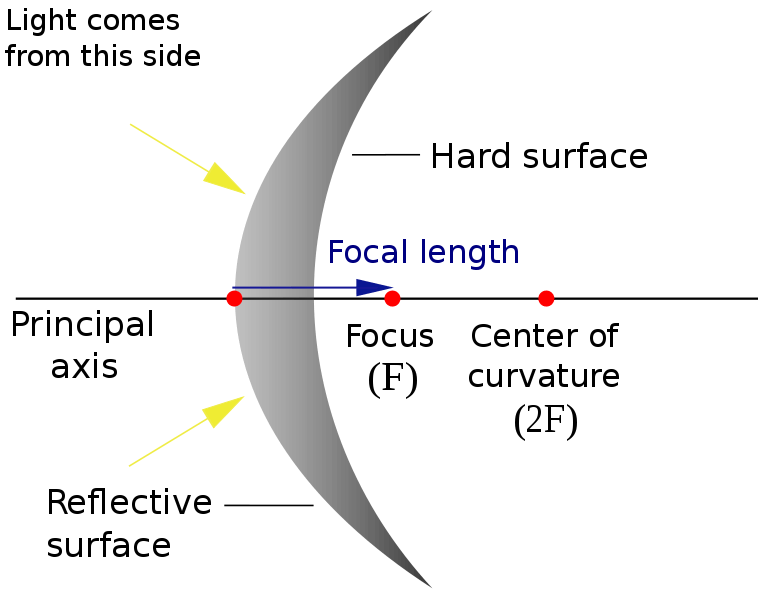
• Pole (P): It’s the geometric centre (or mid-point) of a spherical mirror. (While, geometric centre of a spherical lens is called its Optical Centre)

• Centre of Curvature (C): It’s the centre of the hollow glass sphere of which the spherical mirror is/was a part.

• Radius of curvature (R): It’s the radius of the hollow glass sphere of which the spherical mirror is/was a part.

• Principal Axis: It’s the line joining the pole and the centre of curvature of a spherical mirror. (While in case of a spherical lens, principal axis is the line joining the optical centre and principal focus)

Now, let’s study two major concepts related to spherical mirrors.

Principal Focus and Focal length

When parallel beam of light is incident on a spherical mirror, then:

• In case of a concave mirror, the reflected rays converge at a point on the principal axis, called Principal Focus (F).
  

• In case of a convex mirror, the reflected rays appear to diverge from a point on the principal axis, called Principal Focus (F).

The distance between the Principal Focus (F) and the Pole (P) of the mirror is called the Focal Length (f) of the mirror. It is half of the radius of curvature of the mirror.

That is, Focal length of a spherical mirror (f) = (Radius of Curvature)/2 = R/2

Linear magnification (m)

Linear magnification is the ratio of height of the image (l) formed by a mirror to the height of the object (O). That is, m = \(\frac{l}{O}\).

It is also equal to the ratio of the image distance to the object distance with a negative sign.
That is, m = -v/u = f/(f-u) = (f-v)/f
(where v is the image distance, u is the object distance and f is the focal length of a mirror)

Mirror Formula

If v is the image distance, u is the object distance and f is the focal length of a mirror, then:

1/v + 1/u = 1/f = 2/R

Real and Virtual Images

While studying spherical mirrors and lens, you will often come across the terms – real and virtual images. So, before we move ahead, we should clear our concepts regarding these.

But, first of all, what is an image?

Image is the place/point where the light rays emanating from a point meet after reflection or refraction.

They can be of two types:

• Real Image: The reflected/refracted rays from the original point actually meet/converge at another point.
• Virtual Image: The reflected/refracted rays from the original point do not actually meet/converge at another point, rather they only seem/appear to meet there. That is, they appear to diverge from the image point when produced backwards.

Some cases wherein we can see a real image are:

• images formed on a cinema screen.
• if we place an object in front of a concave mirror, such that it is situated beyond its focus, then we get a real image.

Some cases wherein we can see a virtual image are:

• images formed by a plane mirror.
• if we place an object in front of a concave mirror, such that it is situated between its focus and pole, then we get a virtual image.

Properties of Real and Virtual Images

Now, let’s see the properties of and differences between Real Images and Virtual Images in a bit more detail.

• Real image can only be formed when (reflected or refracted) light rays intersect in real. While, in case of Virtual Image this intersection is only apparent (not real).
• We can see real images on a screen, but not virtual images. (though both of them can be photographed)

Now, let’s get back to our main topic of spherical mirrors.

Position and Nature of images formed by a Concave Mirror

When an object is placed in front of a concave mirror, the position and nature of the image formed will vary based on where the object is placed.

• If the object is at infinity or the incoming rays are parallel to the principal axis, then the image formed by the concave mirror will at its Principal Focus (F).

• If the object is between infinity and Centre of Curvature (C), the image formed by the concave mirror will be between the Principal Focus (F) and the Centre of Curvature (C). The nature of the image will be - real, inverted and smaller in size than the object.
  

• If the object is at Centre of Curvature (C), then the image formed by the concave mirror will at its Centre of Curvature (C) itself. The nature of the image will be - real, inverted and equal in size as the object.
  

• If the object is between Principal Focus (F) and Centre of Curvature (C), the image formed by the concave mirror will be beyond the Centre of Curvature (C). The nature of the image will be - real, inverted and larger in size than the object.
  

• If the object is at Principal Focus (F), then the image formed by the concave mirror will at infinity. The nature of the image will be - real, and infinitely large in size.
  

• If the object is between Principal Focus (F) and Pole (P), the image formed by the concave mirror will be behind the Pole (P). The nature of the image will be - virtual, erect and enlarged.
  

It has been summarized in the table given below:

Position and Nature of images formed by a Convex Mirror

Unlike concave mirrors, the things are much simpler in case of convex mirrors. Image formed by a convex mirror is always virtual, erect and diminished.

• If the object is at infinity, then the image formed by the convex mirror will at its Principal Focus (F).
• If the object is between infinity and Pole (P), the image formed by the convex mirror will be between the Principal Focus (F) and the Pole (P). The nature of the image will be - virtual, erect and diminished.
  

Use of Spherical Mirrors

Now, let’s have a look at some of the uses of spherical mirrors.

Uses of Concave Mirrors

We use concave mirrors:

• to get powerful and focused parallel beams of light, e.g. reflectors and head light in automobiles, search light, hand torches, and table lamps. Doctors also use them to get intense and focused beam of light to examine the insides of eye, ear, mouth etc.
• as shaving mirrors.

Uses of Convex Mirrors

We use convex mirrors:

• to get a larger view of the things behind us, e.g. as rear-view mirrors in automobiles.
  
• to see erect images.