सरल आवर्त गति क्या होती है?

यदि कोई वस्तु अपनी स्थिर/संतुलन माध्य स्थिति से विस्थापित हो जाती है, और उस पर एक बल इस प्रकार कार्य करना शुरू कर देता है कि:

• यह वस्तु को उसकी माध्य स्थिति में वापस लाने का प्रयास करता है, अर्थात बल माध्य स्थिति की ओर निर्देशित होता है, और
• दोलन करने वाले पिंड पर कार्य करने वाले बल का परिमाण माध्य स्थिति से उसके विस्थापन के अनुक्रमानुपाती (directly proportional) होता है। तब ऐसी गति को सरल आवर्त गति (सरल हार्मोनिक गति, Simple Harmonic Motion, SHM) कहते हैं। यह दोलन गति का सबसे सरल प्रकार है।

दोलनशील पिंड पर काम करने वाले किसी निरंतर बाहरी बल के अभाव में, यह कुछ समय में घर्षण, वायु कर्षण, और अन्य विघटनकारी बलों के कारण अपने आप संतुलन की स्थिति में आ जाएगा।

Table of Contents

• वास्तविक जीवन से SHM के उदाहरण
• सरल आवर्त गति से संबंधित कुछ शब्दावली

किसी भी दोलनशील पिंड में एक संतुलन माध्य स्थिति (equilibrium mean position) होती है, और दो चरम छोर होते हैं। आइए इन दो प्रकार की स्तिथियों पर सिस्टम के मापदंडों को समझते हैं।

माध्य स्थिति पर सिस्टम पैरामीटर (System parameters at mean position)

जब सरल आवर्त गति को क्रियान्वित करने वाली एक बिंदु-आकार की वस्तु माध्य स्थिति से गुजरती है:

• वस्तु पर कोई बल नहीं लगता। जाहिर है, इसका मतलब है कि इसका त्वरण (acceleration) शून्य होगा।
• इसका वेग अधिकतम होता है। तो, स्पष्ट रूप से इसकी गतिज ऊर्जा (Kinetic energy) अधिकतम होगी, और इसकी स्थितिज ऊर्जा (Potential energy) न्यूनतम होगी।

चरम छोर पर सिस्टम पैरामीटर (System parameters at extreme ends)

जब सरल आवर्त गति को क्रियान्वित करने वाली एक बिंदु-आकार की वस्तु किसी एक अंतिम छोर पर होती है, तो:

• वस्तु पर लगने वाला प्रत्यावर्तन बल (Restoring force) अधिकतम होता है। जाहिर है, इसका मतलब है कि इसका त्वरण अधिकतम होगा।
• इसका वेग शून्य होता है। तो, स्पष्ट रूप से इसकी गतिज ऊर्जा शून्य होगी, और इसकी स्थितिज ऊर्जा अधिकतम होगी।

वास्तविक जीवन से SHM के उदाहरण

अब, आइए कुछ वास्तविक जीवन प्रणालियों पर एक नज़र डालते हैं जो सरल आवर्त गति (सरल हार्मोनिक मोशन) को प्रदर्शित करती हैं।

नोट

वास्तविक जीवन में कोई भी प्रणाली बिल्कुल शुद्ध सरल हार्मोनिक गति निष्पादित नहीं करती है। ये सभी उदाहरण SHM के उतने ही करीब हैं जितना वास्तविक जीवन में संभव है।

स्प्रिंग के कारण दोलन (Oscillations due to a Spring)

मान लीजिए कि m द्रव्यमान का एक खंड/ब्लॉक क्षैतिज स्प्रिंग से जुड़ा हुआ है (या अनुलंब स्प्रिंग), जो बदले में एक कठोर दीवार से जुड़ी हुई है। इसके अलावा, मान लेते हैं कि जिस सतह पर ब्लॉक को रखा गया है वह घर्षण रहित है।

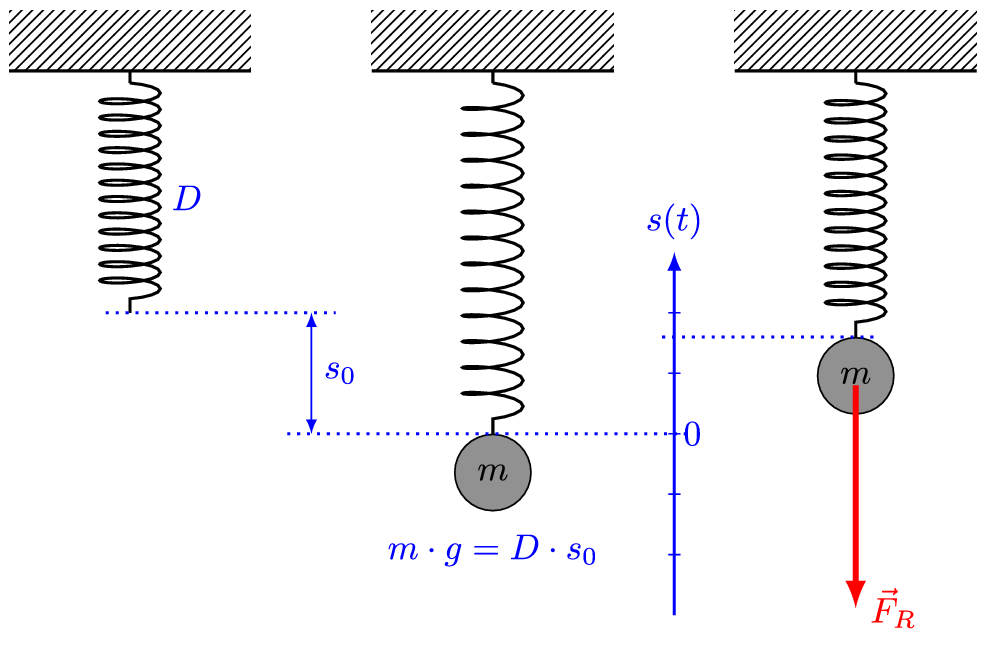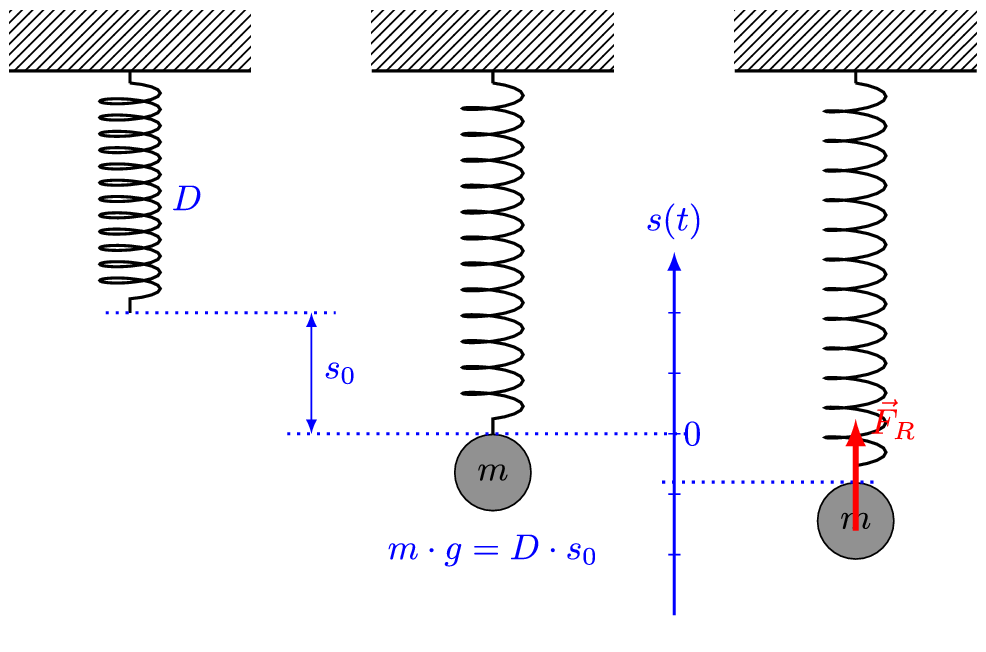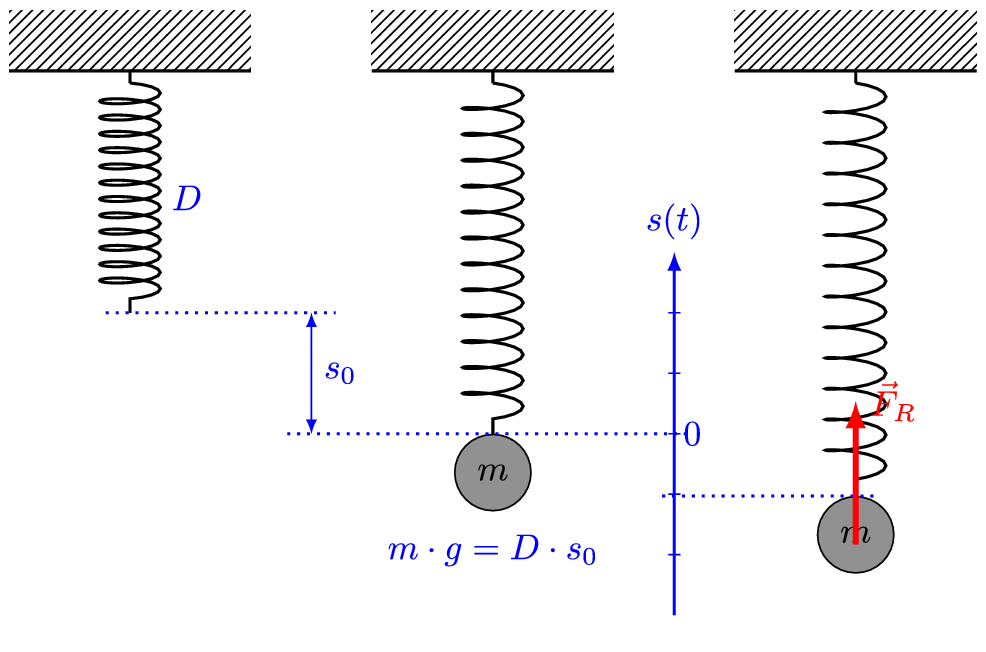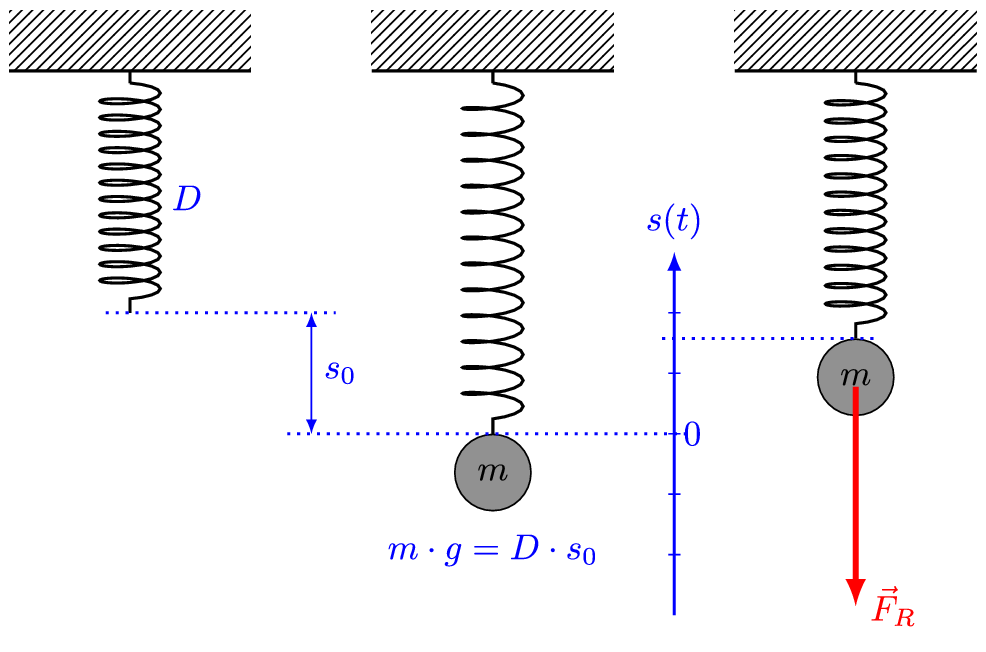
यदि हम ब्लॉक को धक्का देते हैं या खींचते हैं और फिर इसे छोड़ देते हैं, तो यह एक औसत स्थिति (mean position) के आगे-पीछे गति को निष्पादित करेगा, जो सरल आवर्त गति (साधारण हार्मोनिक गति, simple harmonic motion) ही है। अर्थात्, यह एक रेखीय सरल आवर्त दोलक (linear simple harmonic oscillator) के रूप में कार्य करेगा।

इसके पीछे का कारण सरल है। जैसा कि अंग्रेजी भौतिक विज्ञानी रॉबर्ट हुक / Robert Hooke द्वारा खोजा गया था (और हुक के नियम के रूप में प्रस्तावित), कोई स्प्रिंग जब विकृत हो जाती है, तो एक पुनर्स्थापना बल (restoring force) लागू होता है। प्रत्यानयन बल का परिमाण, विरूपण (deformation, अर्थात ब्लॉक का विस्थापन) के समानुपाती होता है। इस प्रत्यानयन बल की दिशा सदैव विस्थापन के विपरीत दिशा में होती है।

सरल लोलक (साधारण पेंडुलम, Simple Pendulum)

मान लीजिए कि m द्रव्यमान का एक खंड/ब्लॉक एक ऊर्ध्वाधर धागे से लटका हुआ है, जो बदले में एक कठोर छत से जुड़ा हुआ है। इसके अलावा, आइए मान लें कि यह एक वैक्यूम में है, यानी कोई वायु कर्षण (air drag) नहीं है।

यदि हम ब्लॉक को धक्का देते हैं या अपनी ओर खींचते हैं और फिर उसे छोड़ देते हैं, तो यह एक औसत स्थिति के इर्द-गिर्द एक झूलती हुई गति (swinging motion) को निष्पादित करेगा, जो एक सरल आवर्त गति ही है। यह एक सरल लोलक (साधारण पेंडुलम, Simple Pendulum) है।

सरल आवर्त गति से संबंधित कुछ शब्दावली

समय सीमा (Time Period)

यह वह समय है जो किसी लोलक (pendulum) को एक पूर्ण दोलन पूरा करने में लगता है। हम इसे निरूपित करने के लिए प्रतीक T का उपयोग करते हैं। और क्यूँकि यह समय को मापता है, इसकी SI इकाई स्पष्ट रूप से सेकंड (second) है।

किसी दिए गए सरल लोलक का आवर्तकाल, T = 2π√(L/g)

जहाँ, L धागे की लंबाई है और g गुरुत्वाकर्षण के कारण त्वरण (acceleration due to the gravity) है।

नोट

ध्यान रखें कि एक सरल लोलक का आवर्तकाल लोलक के द्रव्यमान (mass) पर निर्भर नहीं करता है।

सरल लोलक के विशेष मामले

सरल लोलक के दो विशेष मामले ध्यान देने योग्य हैं।

• अनंत लंबाई का सरल लोलक: यदि एक सरल लोलक के धागे की लंबाई को अनंत बना दिया जाए, तो उसका आवर्तकाल 84.6 मिनट होगा।

• सेकंड लोलक (Second pendulum): यह एक सरल लोलक है जिसका आवर्तकाल ठीक 2 सेकंड होता है।

समय अवधि पर L का प्रभाव

चूंकि किसी भी स्थान पर g लगभग स्थिर होता है, किसी दिए गए सरल लोलक की समयावधि केवल धागे की प्रभावी लंबाई पर निर्भर करती है। आइए इस तथ्य को प्रदर्शित करने वाले कुछ उदाहरण देखें।

• लोलक घड़ी गर्मियों में धीमी और सर्दी में तेज हो जाती है। ऐसा इसलिए है क्योंकि गर्मी के समय में धागे की लंबाई (L) बढ़ जाती है, जिससे समय अवधि (T) बढ़ जाती है।
• यदि कोई बच्चा झूले पर झूलता हुआ खड़ा हो जाता है, तो इससे शरीर का गुरुत्वाकर्षण केंद्र (center of gravity, C.G.) ऊपर की ओर आ जाएगा। इसका अनिवार्य रूप से मतलब है कि स्विंग/झूले की प्रभावी लंबाई (L) घट जाती है। तो, झूले की समयावधि (T) भी घट जाएगी।

समय अवधि पर g का प्रभाव

यद्यपि g किसी भी स्थान पर लगभग स्थिर होता है, यह एक स्थान से दूसरे स्थान पर भिन्न हो सकता है। क्या आप अनुमान लगा सकते हैं कि इसका साधारण लोलक के आवर्तकाल पर क्या प्रभाव पड़ेगा?

आइए देखते हैं।

• यदि g को किसी तरह बढ़ाया जाए (जैसे पृथ्वी के ध्रुवों पर, या जब कोई लिफ्ट त्वरित गति से ऊपर जा रही हो), तो साधारण लोलक का आवर्तकाल कम हो जाएगा, अर्थात यह तेजी से चलेगा।
• यदि g किसी प्रकार घटाया जाता है (जैसे पृथ्वी की भूमध्य रेखा पर, या जब कोई लिफ्ट त्वरित गति से नीचे आ रही हो), तो साधारण लोलक की समयावधि बढ़ जाएगी, अर्थात यह धीमी गति से चलेगी।
• यदि g को किसी तरह शून्य कर दिया जाए (जैसे अंतरिक्ष में किसी कृत्रिम उपग्रह पर), तो सरल लोलक का आवर्तकाल अनंत (∞) हो जाएगा, अर्थात यह कार्य करना बंद कर देगा।

आवृत्ति (Frequency)

एक साधारण लोलक की आवृत्ति उसके द्वारा एक सेकंड में पूरे किए गए दोलनों की संख्या है।

हम इसे निरूपित करने के लिए प्रतीक v का उपयोग करते हैं। इसका SI मात्रक हर्ट्ज़/hertz या \((सेकंड)^{–1}\) है।

आयाम (Amplitude)

हम जानते हैं कि लोलक एक माध्य स्थिति के इर्द-गिर्द घूमता है। इस माध्य स्थिति से उस लोलक की दूरी (किसी भी समय पर) को उसका विस्थापन (displacement) कहते हैं।

किसी झूलते हुए लोलक का आयाम, माध्य स्थिति से अधिकतम विस्थापन होता है। जाहिर है, यह माध्य स्थिति के दोनों ओर बराबर होगा।

हम इसे निरूपित करने के लिए प्रतीक a का उपयोग करते हैं। इसका SI मात्रक मीटर है।

चरण (Phase)

किसी दोलनशील कण का चरण (फेज, Phase) एक भौतिक मात्रा है जो व्यक्त करता है:

• इसकी स्थिति, और
• इसकी गति की दिशा।

इसे निरूपित करने के लिए हम प्रतीक Φ का प्रयोग करते हैं।

तो, दो दोलन करने वाले कण एक ही स्थिति में हो सकते हैं, और फिर भी अलग-अलग चरणों में हो सकते हैं यदि उनकी गति की दिशा अलग हो।

उदाहरण के लिए, SHM को क्रियान्वित करने वाले दो दोलन कणों पर विचार करें जो वर्तमान में अपनी माध्य स्थिति में हैं (इसलिए उनकी स्थिति समान है)।

• यदि वे दोनों एक ही दिशा में भी चल रहे हैं, तो वे एक ही चरण में माने जाएंगे (अर्थात, Φ = 0°)।
• हालांकि, यदि वे विपरीत दिशाओं में आगे बढ़ रहे हैं, तो उनके चरण विपरीत होंगे (अर्थात, Φ = 180°)।